Distribution of Resonance Widths and Dynamics of Continuum Coupling
Open and marginally stable quantum systems are of great current interest in relation to numerous applications in nuclear physics of exotic nuclei, chemical reactions, condensed matter, astrophysics, and quantum informatics. The general problem can be formulated as that of the signal transmission through a complicated quantum system. The complexity of theoretical description of such processes is due to the necessity of a consistent uni.ed theory that would cover intrinsic structure, especially for many-body systems, along with cross sections of various reactions.
One of the best and historically advanced examples of the manifestation of the interplay between intrinsic dynamics and decay channels is given by low-energy neutron resonances in complex nuclei [1]. Interpreting these resonances as quasi-stationary levels of the compound nucleus formed after the neutron capture, agreement was found with predictions of the Gaussian orthogonal ensemble (GOE) of random matrices. With exceedingly complicated wave functions of compound states, the statistical distribution of their components is close to Gaussian.
The neutron decay of these states picks out the specic component related to the channel "neutron in continuum plus a target nucleus in its ground state." The neutron width is proportional to the squared amplitude of this component, and the width distribution is given by the one channel Porter-Thomas distribution (PTD).
Recent experiments with improved accuracy [2] gave evidence of significant deviations from the PTD. The new result was interpreted as a consequence of an unknown nonstatistical mechanism or a breakdown of nuclear theory [3].
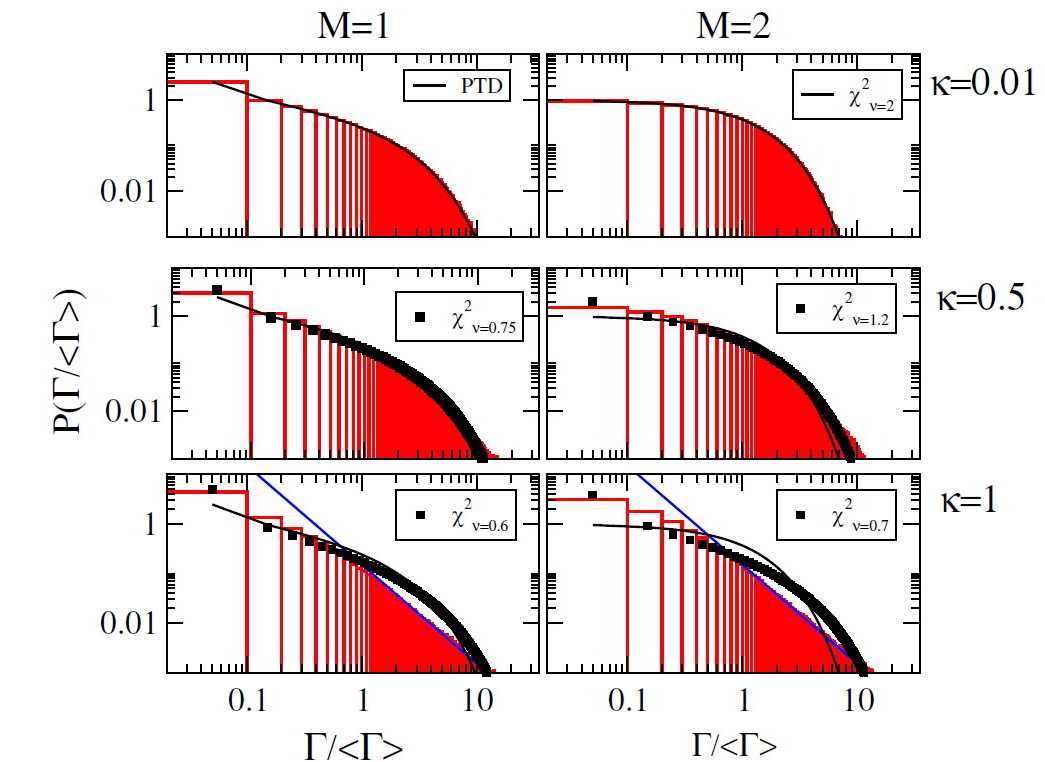
We have shown [4] that a correct description of unstable quantum states in a complicated many-body system naturally leads to deviations from the GOE and PTD, of the same type as observed in [2] Width distributions were analyzed for a system with open channels as a function of the continuum coupling strength. As this coupling increases, the deviation from PTD increases. The figure shows the evolution of the width distributions as a function of the strength of the coupling to one (M=1) and two (M=2) open channels. The pure PTD is shown at the top. The standard PTD is applicable only for extremely narrow resonances. The low-energy neutron resonances in a heavy nucleus correspond to the very beginning of the process of width collectivization. However, already here the deviations from the PTD are noticeable. These deviations are more pronounced for regular intrinsic dynamics than for chaotic intrinsic dynamics. Therefore, the interpretation of the width as a strength of the pure neutron component in the compound wave function fails due to the coupling through continuum that has to be accounted for in a proper statistical description. The phenomenon under discussion is of general nature and it may influence all processes of signal transmission through a quantum system.
References
[1] A. Bohr and B. R. Mottelson, Nuclear Structure (World Scientific, Singapore, 1998), Vol. 1.
[2] P. E. Koehler, F. Becvar, M. Krticka, J. A. Harvey, and K. H. Guber, Phys. Rev. Lett. 105, 072502 (2010). link to journal
[3] E. S. Reich, Nature (London) 466, 1034 (2010).
[4] G. L. Celardo, N. Auerbach, F. M. Izrailev, and V. G. Zelevinsky, Phys. Rev. Lett. 106, 042501 (2011). link to journal