Fringe Effects

Fringe Effect of Dipole

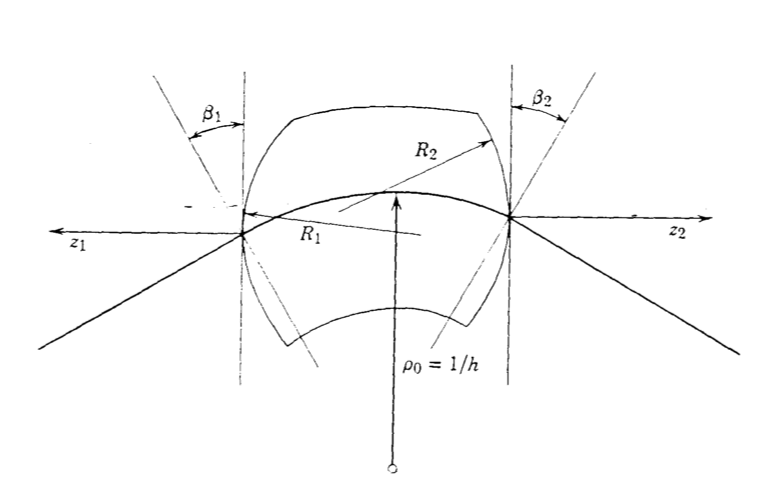
We will model the effect of the dipole edge on the beam. The general edge of a dipole is defined in the above figure, with $\beta_{1/2}$ and $R_{1/2}$ as the angle and radius of the reference particle entrance and exit. In this section we only discuss the effect of the surface angle. In order not to confuse with the betatron function, we use $E_{1/2}$ as the entrance and exit angle below. These are the same notations as the popular modeling tools, such as MADX and Elegant.

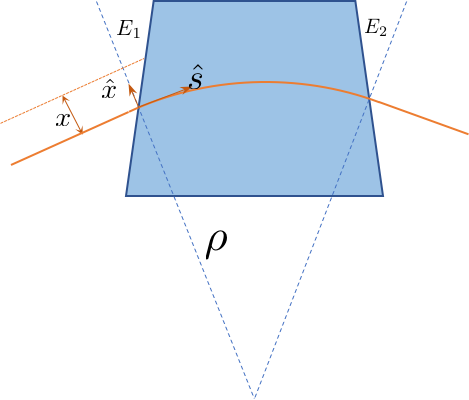Let's consider this simple hard edge model with entrance angle $\theta$. When the pole face is perpendicular to the reference orbit. The dipole is a sector dipole. The transfer matrix is given as

\begin{equation} M_{sector}=\left(\begin{array}{cc} \cos\theta & \rho\sin\theta\\ -\frac{1}{\rho}\sin\theta & \cos\theta \end{array}\right) \end{equation}

If the edge effect can be also represented by a matrix, then the matrix for a non-sector dipole can be written as:

\begin{equation} M=M_{exit}M_{sector}M_{entrance} \end{equation}

The effect in the horizontal plane is straight forward from the above figure. For positive $E_1$, as shown in the figure, a particle with positive $x$ will hit the edge slower than the reference particle. At the time of arrival, the reference already start to rotate. The rotate angle is: $$ \Delta\theta=\frac{x \tan E_1}{\rho+x}\approx \frac{x \tan E_1}{\rho} $$ Here we only keep the linear term.

Equivalently, the particle with horizontal offset at a kick of $\Delta x'=\Delta\theta$. Therefore, the edge effect is similar to a quad:

\begin{align} M_{x,entrance}&=\left(\begin{array}{cc} 1 & 0\\ \frac{\tan{E_1}}{\rho} & 1 \end{array}\right)\\ M_{x,exit}&=\left(\begin{array}{cc} 1 & 0\\ \frac{\tan{E_2}}{\rho} & 1 \end{array}\right) \label{eq:edge_focusing} \end{align}

The vertical edge effect is related to the horizontal one since:

\begin{align} \Delta x'&=-\frac{1}{p_0}\int_{-\Delta t}^{\Delta t} v_zB_y dt\\ \Delta y'&=\frac{1}{p_0}\int_{-\Delta t}^{\Delta t} v_zB_x dt \end{align}

From vanishing curl of the magnetic field, we have $$ \frac{\partial B_x}{\partial y}=\frac{\partial B_y}{\partial x} $$ Then $$ \frac{\partial x'}{\partial x}=-\frac{\partial y'}{\partial y} $$

We get edge focusing matrix for vertical direction as:

\begin{align} M_{y,entrance}&=\left(\begin{array}{cc} 1 & 0\\ -\frac{\tan{E_1}}{\rho} & 1 \end{array}\right)\\ M_{y,exit}&=\left(\begin{array}{cc} 1 & 0\\ -\frac{\tan{E_2}}{\rho} & 1 \end{array}\right) \end{align}

which provides an opposite focusing effect as the horizontal one as in Eq.$\ref{eq:edge_focusing}$