Undulator Radiation

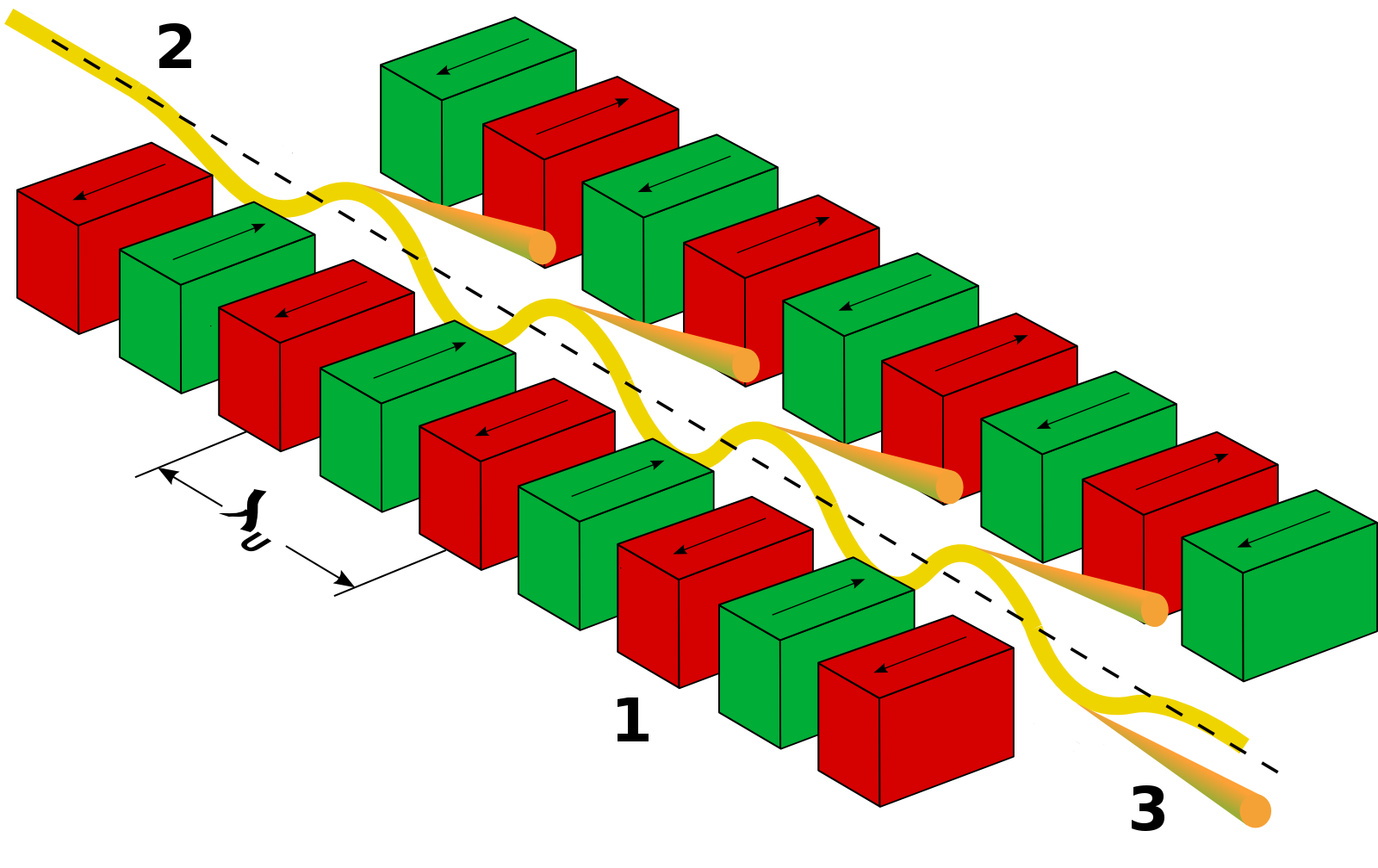
We simply model the undulator as series of dipoles that has alternating field direction, between $\hat y$ and $-\hat y$. The structure repeats every $\lambda_u$ for $N_u$ ($\gg 1$) times. On axis, we may write the magnetic field of an planar undulator as:

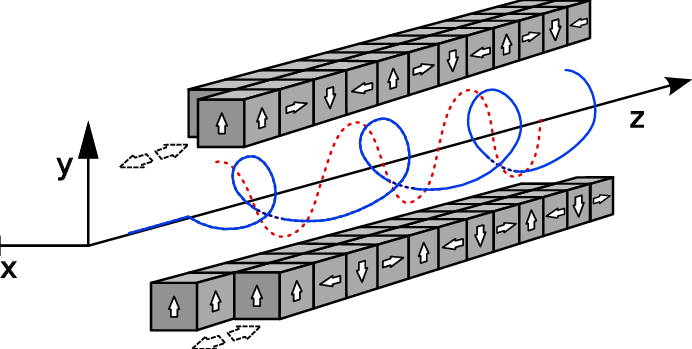
\begin{align} B_y = B_0 \cos \frac{2\pi z}{\lambda_u} \end{align}

There is another type of undulator, name helical undulator. The magnetic field is rotating in the x-y plane. The realization of helical undulator is shown below:

Resonance condition

Let 's use planar undulator as an example to show the resonance condition between the undulator and the relativistic charged particle.

The equation of motion gives:

\begin{align} m\gamma \frac{dv_x}{dt} =- q c B_0 \cos \frac{2\pi z}{\lambda_u} \end{align}

Using the relativistic approximation $z=ct$

\begin{align} \frac{dv_x}{dt} =- \frac {q c B_0}{m\gamma} \cos \frac{2\pi ct}{\lambda_u} \end{align}

Therefore:

\begin{align} v_x &= -\frac {q cB_0 \lambda_u}{2\pi m c\gamma} \sin \frac{2\pi ct}{\lambda_u} \\ &\equiv-\frac{cK}{\gamma}\sin\frac{2\pi ct}{\lambda_u} = - \frac{cK}{\gamma} \sin\left(k_u z\right) \label{vx_in_undulator} \end{align}

Here we define undulator parameter $K$:

\begin{align} K =\frac {q B_0 \lambda_u}{2\pi m c}=0.934 B_0 \text{[Tesla]} \lambda_u \text{[cm]} \end{align}

When $K \ll 1$, we call this undulator; while it is called wiggler when $K \ge 1$.

And the trajectory of the charged particle in the undulator is:

\begin{align} x&=\int v_x dt \\ &=\frac{K\lambda_u}{2\pi c \gamma}\cos\frac{2\pi t}{\lambda_u}\\ &=\frac{K}{k_u \gamma}\cos \left(k_u z\right) \end{align}

Since the magnetic field does not change the energy of the particle, the $z$ component of the velocity is simply:

\begin{align} v_z&=\sqrt{v^2-v_x^2} \\ &=c\sqrt{1-\frac{1}{\gamma^2}-\left(\frac{K}{\gamma}\right)^2 \sin^2\left(k_u z\right)}\\ &=c\sqrt{1-\frac{1+K^2/2}{\gamma^2}+\frac{K^2}{2\gamma^2} \cos\left(2k_u z\right)} \\ &\approx c\left( 1-\frac{1+K^2/2}{2\gamma^2}+\frac{K^2}{4\gamma^2} \cos\left(2k_u z\right) \right) \end{align}

Ignoring the oscillating term, we get the average longitudinal velocity:

\begin{align} \bar{v}_z&=c\left( 1-\frac{1+K^2/2}{2\gamma^2} \right)\\ &=c\left( 1-\frac{1}{2\gamma^{*2}} \right) \end{align}

if we define

\begin{align} \gamma^*=\frac{\gamma}{\sqrt{1+K^2/2}} \end{align}

Then we can study the frequency by Lorentz transformation to the electron rest frame. In this frame, the undulator is 'flying' towards the electrons with relativistic factor $\gamma^*$. Then the radiation becomes dipole radiation with frequency $\lambda'=\lambda_u/\gamma^*$. The frequency spread is $\sim\frac{1}{N_u}$, due to the effect of truncated sinusoidal motion. Then the observer in the lab frame will see this radiation with Doppler frequency shift:

\begin{align} \lambda&=\lambda'\gamma^*\left(1-\beta^*\cos\theta\right)\\ &=\lambda_u\left(1-\left(1-\frac{1}{2\gamma^{*2}}\right)\left(1-\frac{\theta^2}{2}\right)\right)\\ &=\frac{\lambda_u}{2\gamma^{*2}}\left(1+\gamma^{*2}\theta^2\right)\\ &=\frac{\lambda_u}{2\gamma^{2}}\left(1+\frac{K^2}{2}+\gamma^{2}\theta^2\right)\\ \end{align}

Now we reached the resonance condition of the undulator radiation.

Alternative look, Resonance condition

We start with equation of the horizontal velocity

\begin{align} v_x = - \frac{cK}{\gamma} \sin\left(k_u z\right) \end{align}

Suppose we have a planar E-M Wave, which has its electric field expressed as:

\begin{align} E_x &= E_0\exp i{\left(\mathbf{k}_r\cdot\mathbf{r}-\omega_r t\right)} \end{align}

The energy exchange between the electron and the E-M wave gives:

\begin{align} \Delta E&= E_x v_x \\ &=\frac{cE_0K}{2\gamma}\exp i{\left(\left(k_r\cos\theta+k_u\right)z-\omega_r t\right)}+ \frac{cE_0K}{2\gamma}\exp i{\left(\left(k_r\cos\theta-k_u\right)z-\omega_r t\right)} \end{align}

Ignore the fast oscillating term and the phase of the energy exchange, aka, Ponderomotive phase is:

\begin{align} \phi=\left(k_r\cos\theta+k_u\right)z-\omega_r t \end{align}

We specify the resonance condition as: the time derivative of ponderomotive phase vanishes. This condition is written as:

\begin{align} \left(k_r\cos\theta+k_u\right)\frac{dz}{dt}&=\omega_r\\ \left(k_r\cos\theta+k_u\right)\left( 1-\frac{1+K^2/2}{2\gamma^2} \right) &= k_r\\ k_u\left( 1-\frac{1+K^2/2}{2\gamma^2} \right) &= \frac{1+K^2/2+\gamma^2\theta^2}{2\gamma^2}k_r \end{align}

Ignore the second order term, we have:

\begin{align} \lambda_r=\frac{\lambda_u}{2\gamma^2}\left(1+\frac{K^2}{2}+\gamma^2\theta^2\right) \end{align}